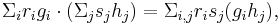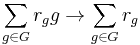Monoid ring

In abstract algebra, a monoid ring is a new ring constructed from some other ring and a monoid.

Definition

Let R be a ring and G be a monoid. Consider all the functions φ : G → R such that the set {g: φ(g) ≠ 0} is finite. Let all such functions be element-wise addable. We can define multiplication by (φ * ψ)(g) = Σ_kl=gφ(k)ψ(l). The set of all such functions φ, together with these two operations, forms a ring, the monoid ring of G over R denoted R[G]. If G is a group, then R[G] denotes the group ring of G over R.

Less rigorously but more simply, an element of R[G] is a polynomial in G over R, hence the notation. We multiply elements as polynomials, taking the product in G of the "indeterminates" and gathering terms:

$\Sigma_i r_i g_i \cdot (\Sigma_j s_j h_j) = \Sigma_{i,j} r_i s_j (g_i h_j),$

where r_is_j is the R-product and g_ih_j is the G-product.

The ring R can be embedded in the ring R[G] via the ring homomorphism T : R → R[G] defined by

T(r)(1_G) = r, T(r)(g) = 0 for g ≠ 1_G.

where 1_G is the identity element of G.

There also exists a canonical homomorphism going the other way, called the augmentation. It is the map η_R:R[G] → R ,defined by

$\sum_{g\in G} r_g g \rightarrow \sum_{g\in G} r_g$

The kernel of this homomorphism, the augmentation ideal, is denoted by J_R(G). It is a free R-module generated by the elements 1 - g, for g in G.

Examples

Given a ring R and the (additive) monoid of the natural numbers N (or {xⁿ} viewed multiplicatively), we obtain the ring R[{xⁿ}] =: R[x] of polynomials over R. The Monoid Nⁿ (with the addition) gives the polynomial ring with n variables: R[Nⁿ] =: R[X₁, ..., X_n].

References

Lang, Serge (2002). Algebra. Graduate Texts in Mathematics 211 ((Rev. 3rd ed.) ed.). New York: Springer. ISBN 0-387-95385-X.